최대공약수 : 두 개 이상의 수의 공약수 중 가장 큰 수
혼자 고민해본 코드
function getGCD(x,y){
let gcd = Math.min(x,y);
while(gcd>=1){
if((x%gcd==0)&&(y%gcd==0)) break;
gcd -= 1;
}
return gcd;
}
console.log(getGCD(10,5)); // 5- 최대공약수는 비교하는 두 수 중 가장 작은 수를 결코 초과하지 않는다.
- 두 수를 비교하여 작은 수를 변수에 저장한다.
- 두 수에 변수의 값을 나누고 나머지를 확인한다.
- 😊 둘 다 나머지 값이 0이라면, 바로 변수 값을 반환한다. ▶ 최대공약수 값
- 🤷♀️ 나머지 값이 하나라도 0이 아니라면, 변수 값을 1씩 빼면서...
나누고 나머지값 비교하고... 1빼고... 나누고 나머지값 비교하고... 1빼고... 나누고 나머지값 비교하고...
▶ 변수의 값이 1이 될 때까지 반복한다.
🤦♀️ 문제점 : 어엄청나게 큰 소수가 하나라도 들어간다면, 어엄청나게 느릴 것이다.
재귀를 활용한 방법 (유클리드 호제법)
두 수 a와 b가 있을 때 (단, a > b) (r ≠ 0)
💛 a % b = 0 일 때, b가 최대공약수이다.
💛 a % b = r 일 때 b % r = 0이라면, r이 최대공약수이다.
💛 a % b = r 일 때 b % r = r`이고, r % r` = 0이라면, r`이 최대공약수이다.
💛 a % b = r 일 때 b % r = r`이고, r % r` = r``이고, r`%r``=0이라면, r``이 최대공약수이다.
.
.
.
💛 r```...``` % 1 = 0 이라면, 최대공약수는 1이다.
위의 내용을 바탕으로 코드짜보기
function getGCD(a,b){
let gcd = (a,b) => a%b==0 ? b : gcd(b,a%b);
return gcd(a,b);
}
console.log(getGCD(10,5)); // 5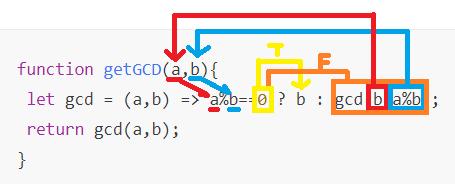
새로 알게 된 것
처음에 유클리드 호제법을 기반으로 코드를 쓸 때, 단, a > b 라는 조건을 지키려 애썼는데...
(Math. 함수를 활용하는 등...)
사실 그럴 필요없었다.
만약... 위의 코드에서 a에 작은 수가 들어가고, b에 큰 수가 들어가더라도
재귀함수를 1회 통과하자마자,
a에 들어있던 작은 수가 b에 들어가고
b에 들어있던 큰 수 가 a에 들어간다.
왜냐면... 작은 수를 큰 수로 나누면, 반드시 그 나머지=작은 수이기 때문이다.
